
格差考察シリーズ第3回。今回の記事では、世帯年収の格差についての統計学的なお話をしたいと思います。
過去記事で色々と考察している過程で、副産物として世帯年収の日本全国におけるランキング推定式が見つかったので最初にご紹介します!
下のグラフが当ブログ算出の、世帯年収300万円~1500万円の範囲における世帯年収順位と上位パーセントを示すものです。おそらく当たらずとも遠からずという精度です。世帯年収だから夫婦合わせた収入としてくださいね!
横軸が年収、縦軸が世帯順位
青い線・・・全50,425,000世帯の中での順位
赤い線・・・上位からのパーセント
*グラフにマウスを合わせると数字が見えます!
(上に出る数字が世帯年収、下に出るのが結果)
2022/6/11追記 スマホでグラフが見えないという報告を貰ったので画像も貼ります。上のグラフが見れなかったらパソコンでアクセスしてみてください。
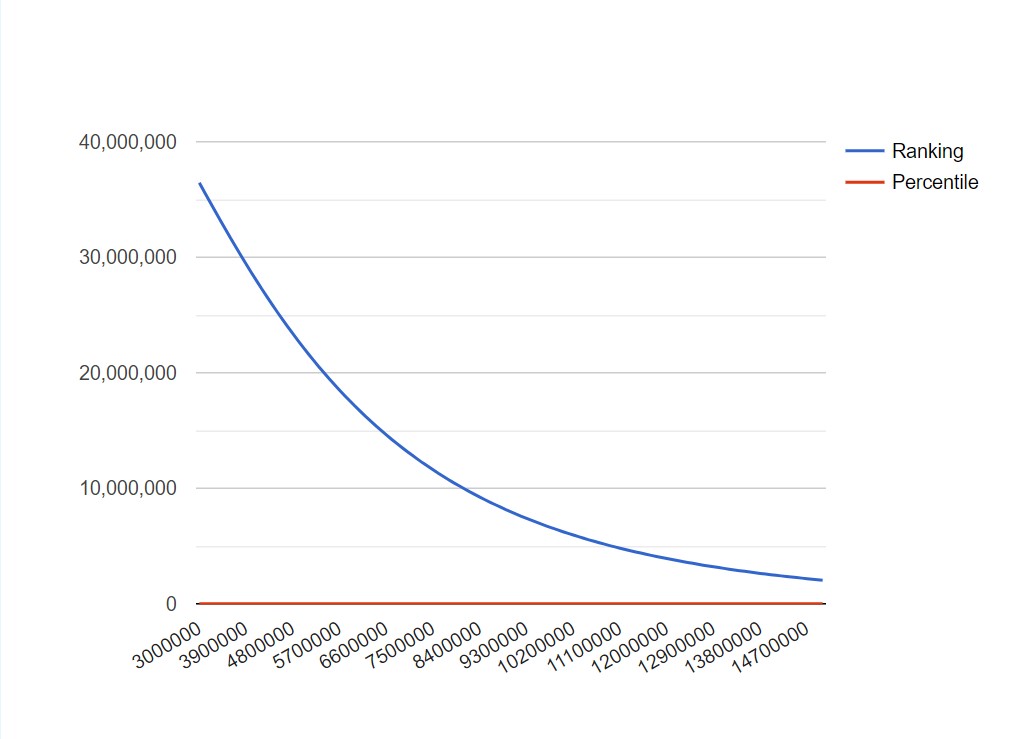
年収300万円未満が範囲にない理由は後述します。あとグラフをきれいに書くために1500万で止めているのですが
「もっと年収貰ってるわ。」
「うちらはパワーカップルや!」
なやんごとなきお金持ちの人はコメントください。結果を返信いたします。
しかしながら今回の記事は人様の家の年収をランク付けしてニヤニヤすることが目的ではありません。
このグラフ、じつは
- 年収の統計書から転記したものではなく!
- 単なる1つの数式をグラフにしたもの
なのであります。にも関わらずなぜ日本の年収ランキングだと胸を張って言い切れるのか?
まずはその算出経緯について説明します。でも難しい数学の話は知らなくていいです!しばしお付き合いを。
実は筆者もあまり数学は得意じゃないです
投資の期待値から割り出した
突然話題が飛んだ中見出しですが、実は冒頭の年収グラフは別記事で算出したランダム投資トレーディングの期待値を表すグラフを調整したものです。
詳しくは前回記事を参照いただきたいですが、こんなルールで取引したものです。
- 1取引あたり、50%の確率で資産の2%を失う/50%の確率で資産が2%増える
- 大人数(無限)がこの取引を延々と繰り返す
- その後の全体的な資産分布を調べる
前回記事を読んでいないとわけがわからないと思いますが、取引ルールを定めて100回取引後、101回取引後…みたいに資産分布の変化を数学的アプローチで全部調べていたんですね。
細かい話を抜きにすると、上記の取引回数が1185回目になったときのデータを平均値560万円になるように調整して、日本人の世帯年収分布の実績値と比べてみたら、なんとほぼ一致したというわけです。
言葉で書いても分かりにくいのでさっそくグラフ化!
まず、これ↓が政府の実測値。政府発表の世帯所得分布(厚生労働省、平成29年)。
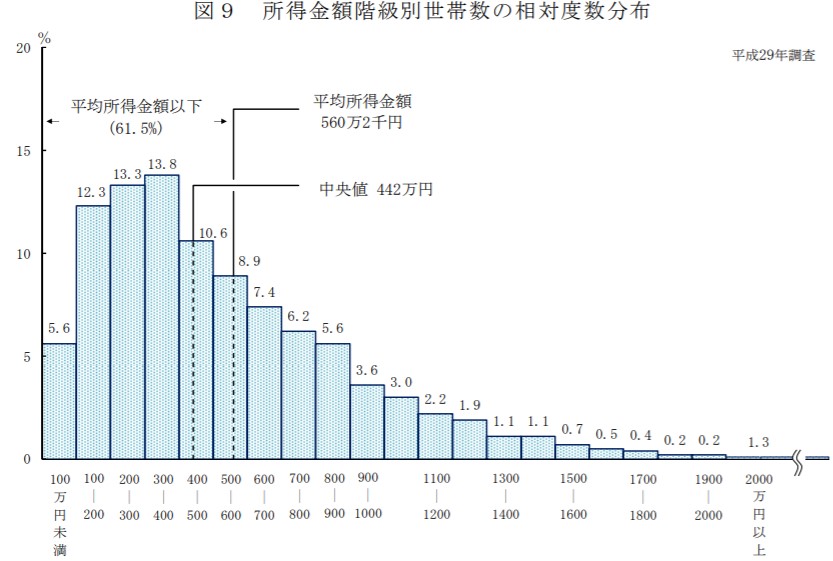
そして↓が当ブログ算出の数式を重ね合わせたもの。
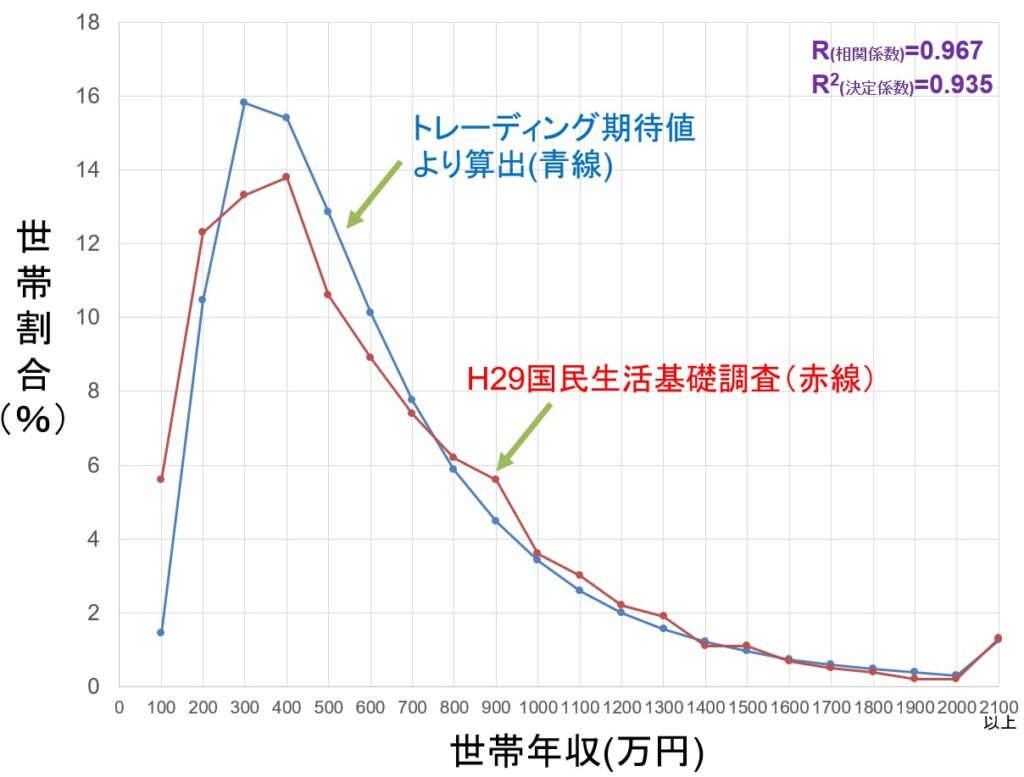
諸々の統計値を算出して並べると下表になります。
| H29国民調査 | ブログ推定式 | |
| 平均値(計算で合わせた軸) | 5602000 | 5602000 |
| 中央値 | 4420000 | 4507406 |
| 平均所得以下 相対割合 | 61.5% | 62.6% |
| 相対的貧困率 | 15.7% | 16.1% |
| GINI係数 | 0.3721 | 0.3740 |
数学的な事はよくわかりませんが、結構ぴったり合っていますね!!
いや~、本当にびっくり。
ただ年収100万円前後のデータはうまく一致しないのですね。そのかわり300万~400万の割合が少し高くなっています。これはおそらく年金生活者とかニートとか、労働自体に積極的に関与しない人たちの影響かなと思っています。もし彼らがフルタイム労働をすれば、分布は当ブログ算出式にもっと一致してくると思います。
(読み飛ばし可!)推定式算出の詳細

ちなみにこのブログ推定式というのはカシオ社の二項分布高精度計算サイトを参考にして作りました。興味を持つ読者さんはゼロだと思いますが、一応厳密性のために書いておきます。下記の式でn=1185, p=0.5と置いています。コンビネーションのCとか懐かしいですね。

(3)upper cumulative distribution(上側累積確率) のx(コイン投げの勝数)はキモとなる数値なのですが、とにかく下画像に書いた式をグルグルっとエクセルで計算したら年収順位が推定できるというわけです。パソコンに書くのが凄まじく面倒なので手書きです。下式への誘導は説明すると長すぎるので割愛です!

メモ帳のサムティしか頭に入りませんでしたが・・
頭に入れなくていいからわざと載せました^^;
重要なのは、上にも書いた「二項分布」という言葉だけです。
それもわからん!
次の章で説明しますね
二項分布と正規分布

さて、
- 政府統計の世帯年収分布
- 今回算出した二項分布が元になるデータ
はとてもよく一致することが分かりました。もう一度おさらいするとこの二項分布というのは
コインの裏表を当てる回数
みたいなイメージで、ランダムに勝敗が決まる行為の積み重ねによって現れます。そしてまさに今回の1185回のように、試行回数が何百回、何千回と増えてくると正規分布に近似される性質を持っています。つまり
世帯年収の分布は概ね正規分布している
と言えるわけです。
ところでリタ犬君は正規分布を知っていますか?
名前は聞いたことがあるが中身はちょっと…
数学的な話は置いておいて、この正規分布というのは自然界のあらゆるところに存在するものなんですね。誤解を恐れずに言うと、例えば
- カブトムシの体長
- タンポポの種が飛んでいく範囲
- 梅雨明けの日付 etc.
みたいな「なんだかよく分からないがばらつきのあるもの」は大体正規分布すると思っておけば8割オッケーでしょう。1枚にするとこのイメージです!
説明がざっくりし過ぎですがイメージはわかりました!
そして今回分かったのは世帯年収もこの例外ではないということです。
じゃあなぜ自然現象や世帯年収は正規分布してしまうのか?それは下記サイトの説明が凄まじく分かりやすいのでコピーして載せておきます(誤字ママ)。
例えば, 上空から地上の定点を狙ってビーズを落としたとします。そのビーズの落下位置のばらつきを考えましょう。無風状態で, ビーズを保持するアームも, 落下装置も, まったく誤差がなければ, すべてのビーズは想定した落下点に命中します。しかし, 風が吹けばビーズは流されるし, アームが振動するれば, それに応じてビーズの落下点が狂います。ビーズの運動が書く要因による影響の積み重ね (線形結合) だとすると, 数多くの影響を積み重ねていくと, 中心極限定理によって正規分布にしたがいます。
引用:自然現象の多くはなぜ正規分布に従うのですか?
年収が正規分布する遠因

それで、ここからが大切なところです。
すなわち、現在の年収というのは過去の数多くのランダムイベントが積み重なって形成された数値なのだろう…と推定できるということなんです。ぱっと思いつく直接的要因は下記のようなものですよね。
- どんな教育をうけたか
- 親はどのような人だったか
- どのような性格が形成されたか
- 知力や体力がどのように育ったか
- どんな企業に就職活動をしたか
これらは当然物凄く年収に影響を与えます。今回のシミュレーションで言うとプラスマイナス50%くらいの利回りがある投資試行と言えるでしょう。
しかしこれ以外にも他愛のない間接的要因、例えば
- 子供のころのある日、公園に遊びに行ったか家にいたか
- 最初に覚えた平仮名はなんだったか
- 学生のころのある日、消しゴムを落としたか落とさなかったか
- 会社での雑用Aと雑用B、どちらを先に済ませたか
これらのようなおおよそランダムと言える小さな出来事だって、巡り巡って人格形成や能力形成、出会う人間に影響しているはずです。たまたま公園で出会った友達に何らかの影響を受けて未来を少し変えることは十分にあるでしょう。
このように、数十年の人生の中で何百万回何千万回も微小なランダム試行を繰り返し、その結果が現在の年収という数値に現れた… →だから(ほぼ)正規分布しているのだ
と考えられるわけです。
資産額は正規分布するのか?

本ブログはアーリーリタイアブログなので年収より資産額が重要です。しかし今回の記事では資産額分布との比較はしていません。ただ、年収が正規分布する限り資産額も正規分布することは自明であろうと思われます。
得られた年収をさらにランダムっぽく蓄財/貯金した累積結果が資産額ですからね!
確かに。
- どこに投資したか
- とある消費をしたか、しなかったか
日々の小さな分岐点の多さは年収の比ではなさそうです。
まとめ
というわけでまとめです。
- ランダム取引シミュレーターの二項分布(からの正規分布近似)は、政府統計の世帯年収分布とよく一致する
- 年収や(おそらく)資産は、恐らく過去の膨大なランダムイベントの積み重ね(線形結合)により形成された数値
なんだか身も蓋もない結論となりました。
そう言われても過去は変えられんし!
しかも過去の事象が現在にどういう影響を与えたのかはよくわかりませんよね。わたしが最初に覚えた平仮名が「の」ではなく「へ」だったら人生が変わっていたかもしれません。「た」だったらバタフライ効果で大金持ちだったかも。今も毎日が運命の分かれ道。

でもこれらを制御するのは不可能なことであります。だって、神様やラプラスの悪魔ならいざ知らず、人間にとってはやはりランダムとしか言えないのですから。考えるだけ無駄というものです。
しかしやはり資産形成は色々な小さなことの積み重ねなのは間違いありません。人生何が起こるかわかりませんが、少なくとも
- 目に見えるリスクを遠ざけ、
- 手を伸ばせば取れるものは全て取る
年収も資産形成も正規分布する自然の一部。人事を尽くして天命を待つしかなさそうです。
でも真面目にやってれば きっと正規分布の神様が見てくれています!
おわり



算数すら苦手なので完全に理解したとは言い難いですが、見えざる手が働いているということですよね…高年収でも貯金無し家庭が何パーセントある、等の記載を見かけますが、それもまさに正規分布のなせる技なのか!興味深いです。まぁ資産は年収よりはコントロールできるのでは?と思いますが。お金無い言い訳に使われそうw
>うさん
コメントありがとうございます!
はい、高年収でも貯金が無い人とか、資産がちゃんとコントロールできるかとか、色々あるわけですが
記事の後半部をかいつまんでいきますと「そのような浪費癖/節約癖がつくかどうか」も成長過程の色々なイベントがランダムで起こって
決まってしまうのではないかということですね。
そういう意味で
>お金無い言い訳に使われそうw
というのは面白いお話で、なんか哲学的な自由意志とか決定論の話になっていきそうですw
政府統計だと測定範囲外になってしまう一定額以上のところを細かく推定するのにも使えそうですね。
>tthさん
いつもコメントありがとうございます!
そうなんです、うまく近似式を作れば年収1億円とか資産5億円とかの極端な人の順位もわかりそうです。
本当はもっと正確な政府統計を貰おうと申し込みをしようとしたんですが一般人には非公開らしく…
またよろしくお願いします!
所得超上位層はkskでトラックしてるはずなので、むしろ国がデータ持ってそうですけど、出さないんですね。なにかやましい事でも…(おっと、こんな時間に荷物か)
資産の方で、修羅の層(w)を細分化できると需要あるんじゃないですかね。というか、私が知りたい。
>tthさん
返事が遅れて申し訳ありません!
そうですね、修羅の層の細分化は知りたい人も多いですよね。
記事では力尽きて算出せず済ませてしまいましたが、やってみようと思います!
取り急ぎ返信までですがまたお願いします!